Sin x в ряд маклорена

1. y = e x .

Имеем f(x) = f'(x) = f»(x) =…= f (n) (x) = e x ;

e x = 1 + х + .

Область сходимости ряда (-∞; ∞).

2. y = sin x.

Очевидно, что производные чётного порядка f (2n) (0) = 0, а нечётного порядка f (2n-1) (0) = (-1) n -1 , i = 1, 2… . По формуле

sin x = x — .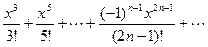

Область сходимости ряда (-∞; ∞).

3. y = cos x.

Рассматривая аналогично, получим

сos x = 1 — .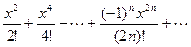

Область сходимости ряда (-∞; ∞).

4. y = (1+x) m , где m — любое действительное число.

(1+x) m = 1 + mx + .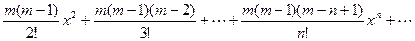

Интервала сходимости ряда (-1; 1).

Ряд называется биномиальным. Если m — целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при n = m+1 m-n+1 = 0, n-й член ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.

Рассмотрим геометрический ряд

= 1 — x + x 2 — x 3 +…+(-1) n x n +…

со знаменателем q = —х, который сходится при | q | = | —x |

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10695 — | 8039 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.

Ряд Тейлора применяют для апроксимации функции многочленами. То есть, линеаризация уравнений проходит путем разложения в ряд Тейлора и отсечения каждого члена старше 1-го порядка.

Определение ряда Тейлора.

Функция f(x) бесконечно дифференцируется в некоторой окрестности т.a:

Этот ряд называется рядом Тейлора функции f в т.a.

Т.е., рядом Тейлора функции f(x) в окрестности точки a является степенной ряд относительно двучлена x — a типа:

Свойства ряда Тейлора.

Если f есть аналитическая функция во всякой точке a, то ряд Тейлора этой функции во всякой точке a области определения f сходится к f в некоторой окрестности a.

Есть бесконечно дифференцируемые функции, ряд Тейлора которых сходится, однако, при этом отличается от функции во всякой окрестности a. Вариант, предложенный Коши:

У этой функции каждые производные в 0 равны нулю, поэтому коэффициенты ряда Тейлора в точке a=0 равны 0.

Если у функция f(x) есть непрерывные производные вплоть до (n+1)-го порядка, то эту функцию можно разложить в степенной ряд по формуле Тейлора:

где R_n − остаточный член в форме Лагранжа определяют так:

Если это разложение сходится в некотором интервале x, т.е. , значит, оно является рядом Тейлора, который представляет разложение функции f (x) в т.a.

Если a = 0, значит, это разложение является рядом Маклорена:

Ряды Маклорена некоторых функций.

1. Экспонента: ,

Если функция (fleft( x
ight)) имеет непрерывные производные вплоть до (left(
ight))-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора : [ ^infty <>left( a
ight)frac <<<<left(
ight)>^n>>><>> > =
ight) + frac <
ight)>^2>>><<2!>> + ldots > + >left( a
ight) <
ight)>^n>>><> + ,> ] где () − остаточный член в форме Лагранжа определяется выражением [ <=»» frac <<
ight)>>left( xi
ight) <
ight)>^>>> <
ight)!>>,>;; рядом Тейлора , представляющим разложение функции (fleft( x
ight)) в точке (a.)

(cosh x =»» sumlimits_^infty >>> < <2n>
ight)!>>
ormalsize> =»» 1 + largefrac<<>><<2!>>
ormalsize + largefrac<<>><<4!>>
ormalsize + largefrac<<>><<6!>>
ormalsize + ldots )

Пусть (fleft( x
ight) =»»
ight)^mu >,) где (mu) − действительное число, и (x
e -1.) Производные будут равны [f»left( x
ight) = mu <1 + x">
ight)^<mu — 1>>,] [f»left( x
ight) = mu left( <mu — 1>
ight) <left( <1 + x>
ight)^<mu — 2>>,] [f»’left( x
ight) = mu left( <mu — 1>
ight)left( <mu — 2>
ight) <left( <1 + x>
ight)^<mu — 3>>,] [ <>left( x
ight) > = <mu left( <mu — 1>
ight)left( <mu — 2>
ight) cdots left( <mu — n + 1>
ight) <left( <1 + x>
ight)^<mu — n>>.> ] При (x = 0,) соответственно, получаем [ ;; <1 + x>
ight)^mu > > =»» <1 + mu x + frac<
ight)>><<2!>> + frac <
ight)left(
ight)>><<3!>> + ldots > +
ight) cdots left(
ight)>><> + ldots > ] Полученное выражение называется биномиальным рядом .

>